

This program terminates for all values of n. Particular values aside, the interesting question is whether we can prove that Time through the loop until it reaches 1. Starting value is a power of two, then the value of n will be even each Particular values of n, we can prove termination. Proof that n will ever reach 1, or that the program terminates. Since n sometimes increases and sometimes decreases, there is no obvious The starting value (the argument passed to sequence) is 3, the resulting If it is odd, the value is replaced by n * 3 + 1.
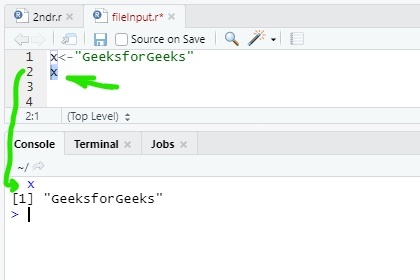
If it is even, the value of n is dividedīy 2. N is 1, which will make the condition false.Įach time through the loop, the program outputs the value of n and thenĬhecks whether it is even or odd. The condition for this loop is n != 1, so the loop will continue until Look at the following function,ĭef sequence ( n ): while n != 1 : print n, if n % 2 = 0 : # n is even n = n / 2 else : # n is odd n = n * 3 + 1 Gets smaller each time through the loop, so eventually we have to get to 0. Know that the value of n is finite, and we can see that the value of n In the case of countdown, we can prove that the loop terminates because we Source of amusement for computer scientists is the observation that theĭirections on shampoo, Lather, rinse, repeat, are an infinite loop. Loop will repeat forever, which is called an infinite loop. The body of the loop should change the value of one or more variables so thatĮventually the condition becomes false and the loop terminates. Loop, the statements inside the loop are never executed. Notice that if the condition is false the first time through the This type of flow is called a loop because the third step loops back around The body consists of all of the statements below the header with the same

Bruce = 5 print bruce, bruce = 7 print bruce


 0 kommentar(er)
0 kommentar(er)
